반응형
1,2,3,9차의 차원(특성)을 가진 input을 통해 과대적합의 그래프의 형태와 Ridge regression을 사용했을 때 어떤 식으로 변화하는지 알아보자
### 1차원 그래프 ###
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
### 1차원 그래프 ###
X = np.arange(1,11).reshape(10,1) # 넘파이 arange 함수 : 배열 만들기
y = np.array([1,7,3,5,13,9,8,11,19,16]).reshape(10,1)
# w.reshape(a, b) : w 배열을 a행, b열 배열로 바꿈
plt.scatter(X,y) # 산점도 만들기
#plt.show()
reg = LinearRegression()
reg.fit(X,y)
y_hat = reg.predict(X)
plt.plot(X, y, 'ro') # 'ro' : 점 그래프(?)
plt.plot(X, y_hat) # 그래프 형식을 명시하지 않으면 선 그래프
plt.show()
|
cs |
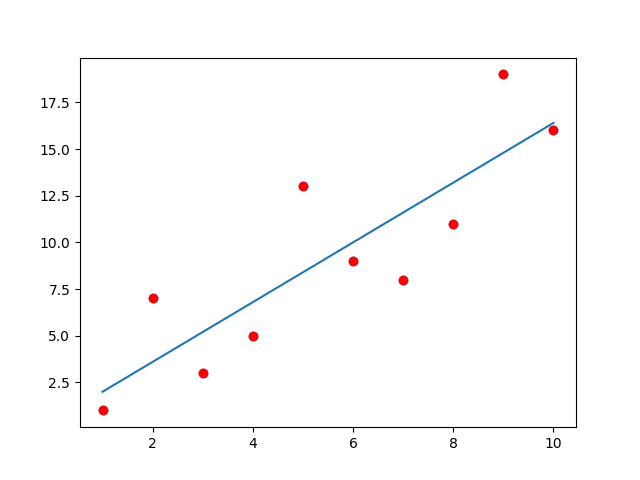
그래프가 직선으로 표현되고 데이터를 정확히 표현하지는 못하지만 나쁘지 않다.
### 2차원 그래프 ###
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
### 2차원 그래프 ###
from sklearn.preprocessing import PolynomialFeatures
# 차원을 변환해주는 라이버러리 임포트
polynomial = PolynomialFeatures(degree=2, include_bias=False)
X_2_poly = polynomial.fit_transform(X) # 특성 X를 2차원으로 변환(특성 한 개 추가)
reg = LinearRegression()
reg.fit(X_2_poly, y) # 두 개의 특성인 X로 모델 훈련
y_2_hat = reg.predict(X_2_poly)
plt.plot(X, y, 'ro')
plt.plot(X, y_2_hat)
plt.show()
|
cs |
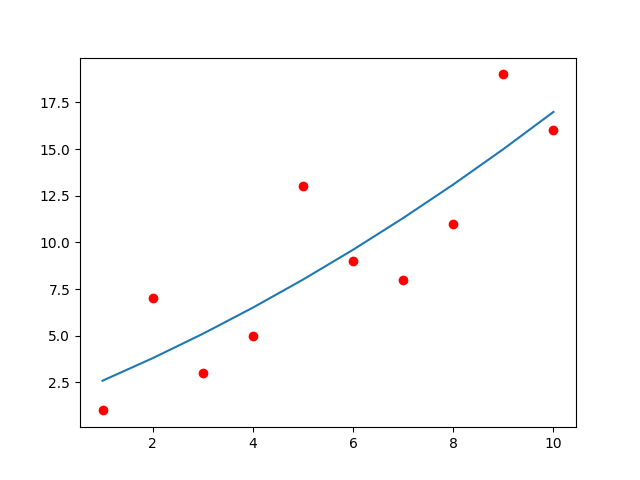
1차원 그래프에 비해 2차원 그래프는 상대적으로 데이터를 잘 표현하고 있다.
### 3차원 그래프 ###
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
### 3차원 그래프 ###
polynomial = PolynomialFeatures(degree=3, include_bias=False)
X_3_poly = polynomial.fit_transform(X) # 특성 X를 3차원으로 변환(특성 두 개 추가)
reg = LinearRegression()
reg.fit(X_3_poly, y) # 세 개의 특성을 가진 X로 모델 훈련
y_3_hat = reg.predict(X_3_poly)
plt.plot(X, y, 'ro')
plt.plot(X, y_3_hat)
plt.show()
|
cs |

앞선 두 개의 그래프보다 더 낫다고 할 수 있따. 지금의 상황에서는 최선으로 보인다.
### 과대적합이 된 경우 ###
|
1
2
3
4
5
6
7
8
9
10
11
12
|
### Overfitting 된 경우 ###
polynomial = PolynomialFeatures(degree=9, include_bias=False)
X_9_poly = polynomial.fit_transform(X) # 특성 X를 9차원으로 변환
reg = LinearRegression()
reg.fit(X_9_poly, y) # 아홉 개의 특성인 X로 모델 훈련
y_9_hat = reg.predict(X_9_poly)
plt.plot(X, y, 'ro')
plt.plot(X, y_9_hat)
plt.show()
|
cs |
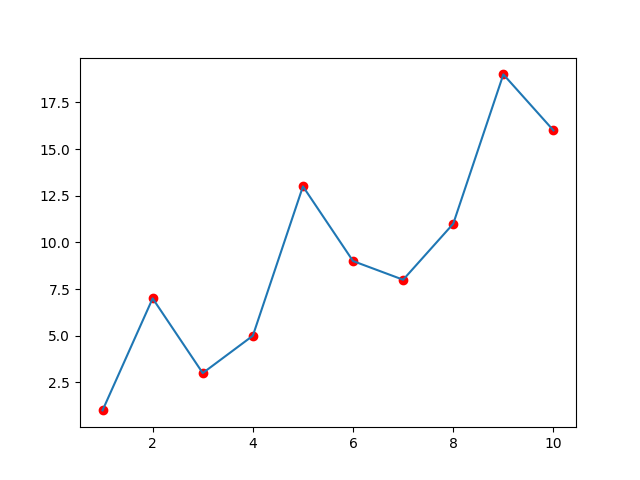
과대적합된 상황을 표현하기 위해서 특성이 9개로 훈련하였다.
그래프에서 볼 수 있듯이 예측값과 데이터의 오차는 0에 수렴한다. 하지만 너무 지금의 상황에만 맞춰져 있어서 새로운 예측을 했을 때 틀릴 가능성이 매우 높다. 이것이 과대적합된 상황이다.
### Ridge regression ###
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
### Overfitting 방지 ###
### 규제, Ridge regression 사용 ###
from sklearn.linear_model import Ridge
#Ridge 라이브러리
ridge = Ridge(alpha=1.0) # alpha = 하이퍼파라미터 람다, 클수록 규제가 강함
ridge.fit(X_9_poly, y)
y_hat_ridge = ridge.predict(X_9_poly)
plt.plot(X, y, 'ro')
plt.plot(X, y_9_hat)
plt.plot(X, y_hat_ridge)
plt.show()
|
cs |
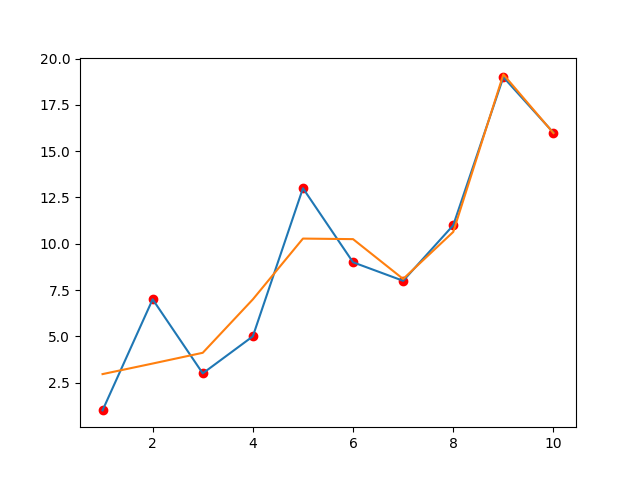
앞서 과대적합된 상황 (특성이 9개)과 동일한 상황이지만 Ridge regression을 사용하였다.
노란색으로 표시된 부분이 규제를 사용한 부분인데 기존의 상황(파란색)과 차이를 보인다.
규제를 사용한 부분은 예측값과 데이터의 오류는 기존의 상황보다는 많지만 좀 더 일반화된 모델로 생각할 수 있다.
반응형
'ML 실습' 카테고리의 다른 글
| Performance metrics를 통해 모델 성능 평가하기 - 정확도(Accuracy), 재현율(Recall), 정밀도(Precision), F1 score (0) | 2023.01.26 |
|---|---|
| 선형 회귀를 이용해서 특성이 두 개 이상인 데이터 예측하기 (0) | 2023.01.14 |