군집(clustering)은 label (정답)이 없는 상황에서 사용하는 비지도학습의 예이다.
모델 스스로 데이터들 간의 상관관계를 찾아서 비슷한 것끼리 묶는(군집) 방법으로 모델을 만든다.
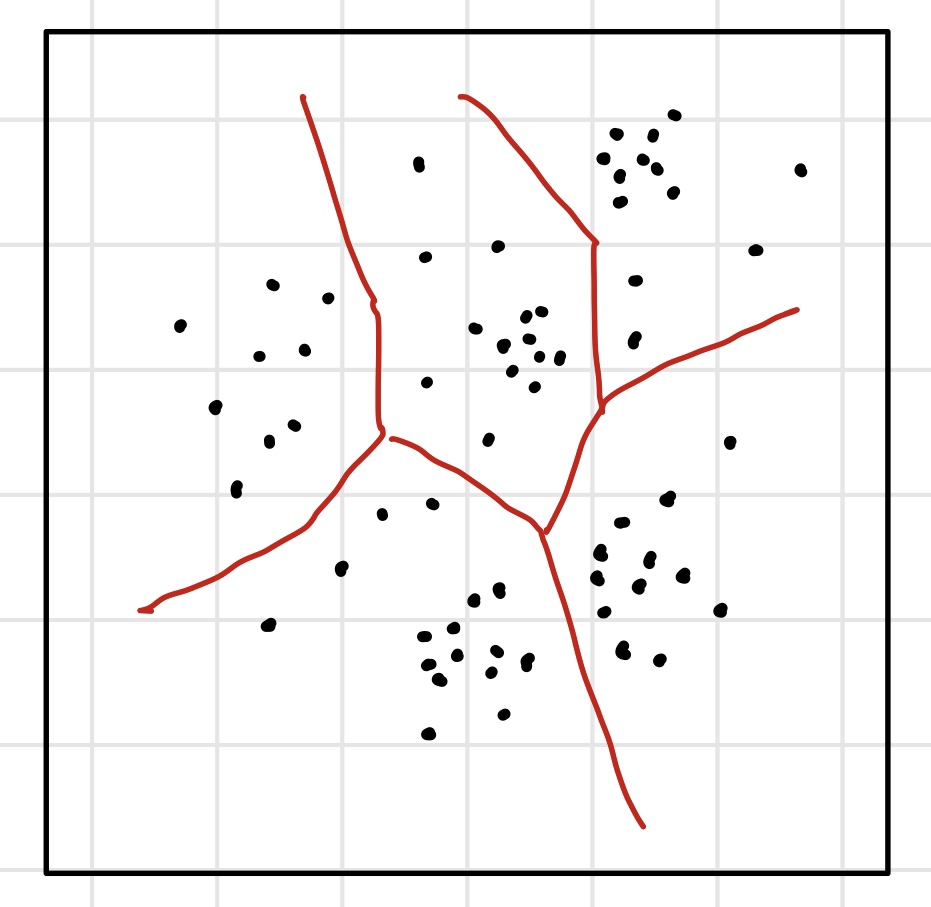
데이터가 2차원으로 표현가능하다고 가정하자.
위의 그림처럼 데이터가 분포되어 있을 때 결정경계(빨간색)를 찾고, 새로운 데이터가 들어오면 어떤 그룹 속해 있는 것인지 판단하는 것이 군집의 목적이다.
### K-mean 알고리즘 ###
군집에서 많이 사용되는 알고리즘 중 하나가 K-mean 알고리즘이다.
그렇지 않은 다른 향상된 알고리즘이 있다고는 하지만 기본적으로 K-mean 알고리즘에서는 K(몇개의 그룹으로 나눌 것인지)를 사용자가 지정해주어야 한다.
밑의 상황에서는 K=5이다.

K-mean 알고리즘에서는 평균(mean)을 사용한다.
μ1 ... μ5(파란색)이 각 그룹의 평균이다.

k번째 평균 μk는 위와 같이 구한다.
μ를 구하면 새로운 데이터가 들어왔을 때 어떤 그룹에 속해있는지 판단할 수 있게된다.

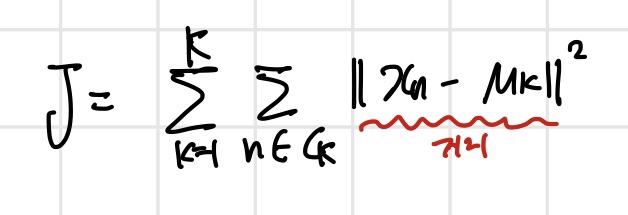
새로운 데이터 xn과 μk와의 거리를 최소화 해야하는 비용함수로 정의함으로써 적절한 모델을 만들고 xn이 어디에 속해있는지 판단할 수 있는 것이다.
xn 과 가장 가까운 μk를 찾고 그 μk가 속해있는 그룹에 xn도 속해있다고 판단한다.
그런데 이러한 과정을 하기위해서는 μk와 μ가 어디에 속해있는지 그룹, 그룹을 나누는 결정경계를 모두 알아야한다.
어떻게하면 이것을 구할 수 있을까?
몇가지의 과정을 반복적으로 수행함으로써 구할 수 있다.

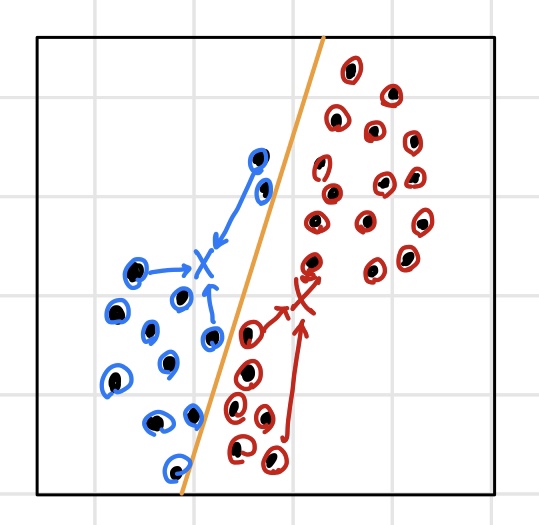

1. 결정경계와 μ(center)가 없는 상황에서 임의의 center를 지정한다.
2. center와 데이터의 거리를 통해 결정경계를 만들고 데이터를 그룹화한다.
3. 그 그룹 안에서의 새로운 center를 찾는다.
4. 새로운 center를 기준으로 다시 데이터와의 거리를 통해 새로운 결정경계를 만들고 데이터를 그룹화한다.
이러한 과정을 정확한 center와 그룹이 찾아질 때까지 반복한다.
이것이 k-mean 알고리즘이다.
k-mean 알고리즘에는 단점이 존재한다.
1. 초기의 상황에 민감하다. (초기에 선택한 상황에 따라 결과가 많이 달라질 수 있다)
2. K(데이터를 몇개의 그룹으로 나눌 것인지)를 사용자가 선택해야한다.
3. Convex(볼록)한 상황에서만 동작가능하다.
Convex?
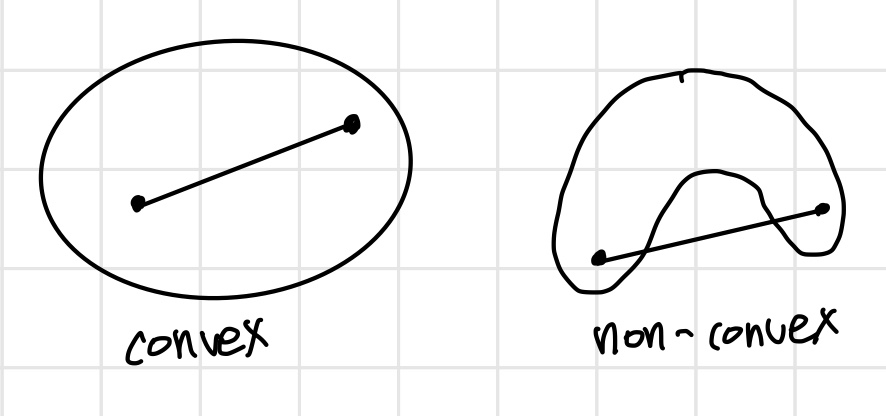
왼쪽에서처럼 내부에서 임의의 두 점을 선택해서 직선을 그렸을 때 그 직선이 항상 내부에만 존재하면 convex(볼록)하다고 한다.
군집(clustering)에서 보면

k-mean 알고리즘을 사용하면 왼쪽과 같이 convex한 형태의 그룹만을 얻을 수 있고 오른쪽에서처럼 non-convex한 그룹은 얻을 수 없다.
'머신러닝' 카테고리의 다른 글
| 차원 축소(Dimensionality Reduction), PCA (0) | 2023.01.31 |
|---|---|
| Suport Vector Machine(SVM, 서포트 벡터 머신), 최대 마진 분류 (2) | 2023.01.29 |
| Kernel Ridge Regression(KRR) (0) | 2023.01.28 |
| Kernel method, feature space(특성 공간) (0) | 2023.01.27 |
| 앙상블 학습, Random Forest 개념 (0) | 2023.01.26 |