Ridge regression, 교차검증(cross validation)
Ridge regression은 규제(regularization)의 방법 중 하나로 2 norm을 사용한다.

위의 식이 최소가 되는 가중치 W와 하이퍼파라미터 Λ를 찾는 것이 목적이다.

regularizer에서 보이는 2norm은 위의 그림과 같이 상수 B로 규제한다.

w가 2차원 벡터 즉 w T= [ w0, w1 ] 일 때
2norm 이 뜻하는 것은 w0^2 + w1^2 = B(상수) 이다. 이것은 평면 위에 놓인 반지름이 루트B인 원을 뜻한다.

다음으로 2차원 벡터일 때 square loss(빨간색)를 그래프로 표현하면 위의 그림과 같이 3차원의 면으로 표현할 수 있다. 그것을 위에서 본 그래프가 하늘색으로 표시된 그래프이다.
우리는 상수 B를 통해 가중치 W의 크기를 규제하고(B보다 작도록) 평면에서 표시된 2norm의 위에 square loss가 있을 때 그것을 solution이라고 한다(파란색 점).
이렇게 함으로써 규제된 가중치 W를 찾을 수 있는 것이다.

다시 식으로 돌아가서, 위의 식이 최소로 만들기 위해서는 적절한 가중치 W와 하이퍼파라미터 Λ를 찾아야한다.
1. 적절한 가중치 W찾기
2. 적절한 하이퍼파라미터 Λ 찾기
1. 적절한 가중치 W를 찾기 위해서는 앞의 Least squre에서 썻던 방법과 동일한 방법을 사용한다. 전체 식을 w로 미분한 후 미분 값이 0이 되는 W를 찾는다.
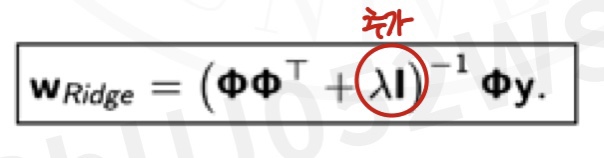
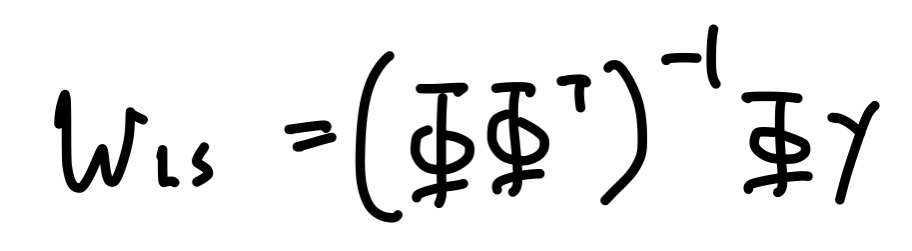
Least squre와 비교한다면 식에 ΛI가 추가되었다. I는 단위 행렬이다.
2. 적절한 하이퍼파라미터 Λ를 찾기위해서는 교차검증(cross validation)을 사용한다.

훈련 데이터 세트을 임의의 수로 등분한 한다. (예시는 5등분)
첫번째 세트을 빼고 나머지 4개로 훈련한 후 Validation(훈련에 참여하지않은 첫번째 세트)와 비교해서 Validation error를 찾는다.
마찬가지로 다섯번째 세트까지 동일한 과정을 한 후 Error의 평균을 계산한다. 이것을 Validation error라고 한다.
적절한 하이퍼파라미터 Λ를 찾기 위해서는 여러 번의 교차검증 과정을 반복한다.
특정한 Λ를 선택한 후 교차검증을 수행해서 그때의 Validation error를 찾고
다른 Λ를 선택한 후 같은 과정을 반복한다.
여러번 반복하다가 Validation error가 가장 작은 Λ를 선택해서 최적의 하이퍼파라미터 Λ를 선택할 수 있다.