Lasso

Lasso는 Ridge regression과 마찬가지로 규제(regularization)의 한 종류이다.

 

우선 Lasso를 통해 얻은 가중치 W는 다음과 같다.

Least squre를 통해 얻은 squre loss는 Ridge regression과 똑같이 사용하지만 다른 점은 패널티 항에 있다.

Ridge regression에서는 패널티 항을 2Norm을 사용했지만 Lasso에서는 1Norm을 사용한다는 것이 가장 큰 차이이다.

 

마찬가지로 1Norm의 크기를 조정해서 찾고자 하는 가중치 범위를 제한한다.

 

 

 

Lasso를 이해하기 위해서는 Sparseness를 알아야한다.

Sparseness는 단어 뜻은 "드문드문함", "산재함"이라고 하는데 위의 그림에서처럼 가중치 W의 값이 0이 된 값이 많아서 실제로 사용될(0이 아닌) 가중치, 특성은 적은 상태를 말한다. 

 

예를 들어 100개의 특성을 가진 데이터가 있을 때 80개의 가중치 W가 0이면 나머지 20개의 특성만 사용해서 훈련에 사용할 수 있다.

 

이러한 sparseness 상태를 만드는 것이 Lasso의 목표이다.

 

 

따라서 1Norm을 사용한다.

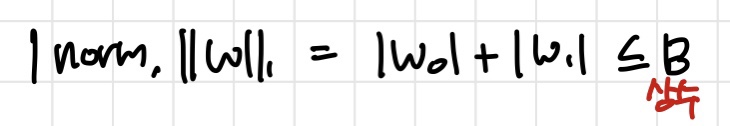
W가 2차원 벡터이면 1Norm W를 위의 식과 같이 각각의 절대값의 합으로 표현할 수 있다.

 

따라서 마름모 꼴(빨간색)로 평면에 나타낼 수 있다.

Ridge regression에서 2Norm을 사용할 때는 원으로 나타낼 수 있었다.

 

마찬가지로 squre loss를 위에서 바라봤을 때 파란색 타원으로 나타낼 수 있는데 squre loss와 1Norm이 처음 만나는 지점(노란색 점)을 살펴보면 좌표가 (w0, 0)인 것을 알 수 있다. 즉 w1이 0이 된 것이다.

 

특성이 더 많아지면 w가 0이 되는 상황이 더 많아질 것이다.

 

이처럼 많은 w를 0이 되게하는 상황 (sparseness)를 만들기 위해 Lasso에서는 1Norm을 사용한다.

 

 

 

 

 

Ridge regression과 Lasso의 차이를 알아보자.

Ridge regression에서는 하이퍼파라미터 Λ가 커지면 전체적으로 가중치 w값이 감소해서 결국 한 점에서 w가 0이된다.

하지만 Lasso에서는 각각의 가중치마다 w가 0이되는 점이 다르다. 

Λ가 커지면서 w가 한 개씩 0이된다. 즉 고려할 특성이 한 개씩 적어진다는 것을 뜻한다.

 

Lasso 그래프에서 빨간색 점선으로 표시한 부분을 보면 총 특성은 n개여서 가중치는 n개이다. 하지만 w1, w2, w3를 제외한 n-3개의 가중치 w들은 0이되어서 더이상 고려할 필요가 없다.

 

즉 특성 3가지만 고려하면 된다는 것이다. 

 

이것이 Lasso를 사용하는 이유이다.