우선순위 큐 : 우선 순위를 가진 항목을 저장하는 큐
가장 일반적인 큐로 생각할 수 있다. - 가장 마지막으로 들어온 데이터가 우선순위가 높음 -> 스택
- 가장 먼저 들어온 데이터가 우선순위가 높음 -> 큐
우선순위 큐는 힙(Heap)을 이용해서 구현한다.
힙(Heap) ?
완전 이진트리, 반 정렬, 우선 순위 큐를 위한 자료구조.

힙에는 최대 힙(MaxHeap) 과 최소 힙 (MinHeap)이 있는데
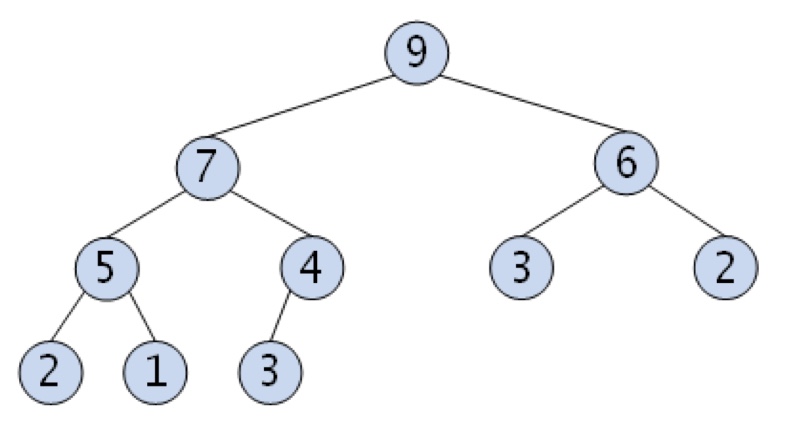

최대힙 : 부모노드의 key > 자식노드의 key, 가장 위에 있는 값(인덱스 1)이 최대 값
최소힙 : 부모노드의 key < 자식노드의 key, 가장 아래에 있는 값(인덱스 1)이 최소 값
힙의 높이 : O(logn) , n은 노드의 개수
힙은 배열을 이용해서 구현할 수 있는데 가장 위에 있는 노드(우선순위가 가장 높음)의 인덱스는 1로 설정했다.

그리고 부모 노드와 자식 노드의 인덱스 간의 관계가 있는데
부모노드의 인덱스 = 자식노드의 인덱스 / 2
왼쪽 자식노드의 인덱스 = 부모노드의 인덱스 * 2
오른쪽 자식노드의 인덱스 = 부모노드의 인덱스 * 2 + 1
### HeapNode ###
|
1
2
3
4
5
6
7
8
9
10
11
|
#pragma once
#include <iostream>
class HeapNode {
private:
int key;
public:
HeapNode(int k = 0) : key(k) {}
void setKey(int k) { key = k; }
int getKey() { return key; }
void display() { printf("%4d", key); }
};
|
cs |
### MaxHeap Class, insert ###
삽입연산 : 삽입할 노드를 가장 말단에 놓고 자신의 위치에서 한 층 위(부모)의 노드와 값을 비교하면서 적절한 자신의 자리를 찾아감 ( 올라가며 )
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#pragma once
#include "HeapNode.h"
#define MAX_ELEMENT 200 // 배열로 구현했기 때문에 최대 크기 지정
class MaxHeap {
private:
HeapNode node[MAX_ELEMENT];
int size;
public:
MaxHeap() : size(0) {}
bool isEmpty() { return size == 0; }
bool isFull() { return size == MAX_ELEMENT - 1; }
HeapNode& getParent(int i) { return node[i / 2]; }
HeapNode& getLeft(int i) { return node[i * 2]; }
HeapNode& getRight(int i) { return node[i * 2+1]; }
void insert(int key) {
if (isFull()) return;
int i = ++size;
// 삽입하는 데이터의 인덱스는 현재 사이즈의 최대 +1
// 마지막 순서로 일단 삽입
while (i != 1 && key > getParent(i).getKey()) {
// 삽입하는 값이 부모의 값보다 작을때까지 반복
// 부모의 값과 자신의 값을 비교하면서(마지막 순서에서 위 순서로
// 올라가면서) 값의 위치를 찾는 과정
node[i] = getParent(i);
i = i / 2;
// 삽입하는 값이 부모의 값보다 크면 부모 노드를 밑으로 내리고
// 삽입하는 값의 인덱스를 2로 나눔(인덱스를 한 층 올림)
}
node[i].setKey(key);
// 위치를 찾으면 데이터 삽입
}
|
cs |
### remove ###
삭제연산 : 가장 위에 있던(인덱스가 1인) 노드를 삭제하고 가장 말단에 있던 노드를 가장 위로 올린 후 자신의 위치에서 한 층 아래(자식)의 노드와 값을 비교하면서 적절한 자신의 자리를 찾아감( 내려가며 )
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
HeapNode remove() {
if (isEmpty()) return NULL;
HeapNode item = node[1];
// Heap에서 가장 위에 있었던 노드, 삭제할 노드
HeapNode last = node[size--];
// 배열의 마지막에 있던 노드를 연산에 사용
int parent = 1;
int child = 2;
// 노드 값 비교를 위해서 초기에 설정한 인덱스 값
while (child <= size) {
if (child < size && getLeft(parent).getKey()
< getRight(parent).getKey())
// 부모노드의 왼쪽 자식, 오른쪽 자식 중 어떤 값이 더 큰지 비교
child++;
// 비교 후 오른쪽 자식의 값이 더 크면 +1
// 오른쪽 자식의 인덱스가 왼쪽 자식의 인덱스보다 1 크기 때문에
// 인덱스에 1을 더한다는 의미는 오른쪽 자식을 뒤에 나올 연산의 인덱스로 사용한다는 의미
if (last.getKey() > node[child].getKey()) break;
// 배열의 마지막에 있던 노드의 값과 선택된 자식 노드의 값을 비교해서
// 마지막에 있던 노드(last)의 값이 더 크면 while문을 빠져나옴 -> 위치를 찾음
node[parent] = node[child];
// 자식노드를 부모노드로 설정 -> 한 층 올림
parent = child;
child = child * 2;
// 부모노드, 자식노드의 인덱스 재설정 -> 아래 층에서 재비교를 하기 위함
}
node[parent] = last;
// 찾은 위치에 last 노드 삽입
return item;
// 삭제한 노드(맨 위에 있던 노드) 반환
}
|
cs |
### display ###
|
1
2
3
4
5
6
7
8
9
10
|
void display() {
for (int i = 1, level = 1; i <= size; i++) {
if (i == level) {
printf("\n");
level *= 2;
}
node[i].display();
}
printf("\n-----------------------------");
}
|
cs |
### 힙 정렬 ###
정렬되어 있지않은 배열을 힙에 전부 삽입한 후 차례로 삭제하면 정렬이 됨
|
1
2
3
4
5
6
7
8
9
10
11
12
|
void heapSort(int a[], int n) {
MaxHeap h;
// 힙 정렬을 위해 사용할 heap
for (int i = 0; i < n; i++) {
h.insert(a[i]);
}
for (int i = n - 1; i >= 0; i--) {
a[i] = h.remove().getKey();
}
}
|
cs |
'자료구조' 카테고리의 다른 글
| [자료구조] 인접 행렬로 구현한 그래프 (0) | 2022.12.03 |
|---|---|
| [자료구조] 그래프 (0) | 2022.12.03 |
| [자료구조] 이진탐색트리 삭제 연산 (0) | 2022.11.18 |
| [자료구조] 이진탐색트리, BinarySearhTree 개념, 탐색, 삽입 (0) | 2022.11.15 |
| [자료구조] 수식 트리 (0) | 2022.11.11 |